| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- cs231n
- 백준 1339 자바
- 1916
- 알고리즘
- 머신러닝
- 백준
- 자바
- 짝지어제거하기
- 논문
- dijkstra
- 다익스트라
- deeplearning
- 관심사분리
- NLP
- 논문구현
- 3745
- 클린코드
- 디미터법칙
- Java
- MachineLearning
- Alexnet
- 딥러닝
- 백준 1916 자바
- 1107번
- 1261
- GPT
- 백준9095
- 백준 1339
- 논문리뷰
- 알렉스넷
- Today
- Total
산 넘어 산 개발일지
[CS231n - Lecture 7] Training Neural Networks - Part II 본문
[CS231n - Lecture 7] Training Neural Networks - Part II
Mountain96 2021. 8. 11. 16:22Optimization
가중치를 최적화하는 방법, 혹은 가중치를 업데이트하는 방법을 말한다. Optimization에도 여러가지가 있다. 각 Optimization은 이전 기법의 단점을 보완하는 형태로 등장했고, 최근에는 어느 한 가지가 좋다!라는 느낌보다는 상황에 따라서 골라서 사용하는 추세이다.
SGD
가장 초기에 사용된 optimizer이다. 기존의 Gradient Descent의 경우 한 번 학습할 때 모든 데이터를 봐야 하는데 이 때문에 속도가 너무 느려서 고안되었다. SGD는 전체 데이터에서 mini-batch라는 소규모 그룹을 뽑아서 이들을 가지고 loss를 계산한 뒤 가중치를 갱신하는 것이다. 그러나 다음과 같은 상황에서 문제가 발생한다.

이렇게 최적점을 찾아가는데 진동 현상이 있을 수 있다. 이는 한 번 학습할 때마다 Loss가 계속해서 크게 바뀌는 경우를 나타내는 것 같다. 이 경우 SGD는 최적점에 도달하기까지 굉장히 오랜 시간이 걸리게 된다.

또 다른 문제는 local minima에 걸리거나 saddle point에 걸리는 경우다. 만약 loss function이 이런 현상이 닥치면 gradient가 0이 되고, 결국 거기서 더 나아가지 못할 것이다. 그리고 local minima보다는 saddle point가 실제 고차원적인 학습을 진행할 시에 더 빈번하게 발생한다고 한다.
Momentum

이러한 SGD의 문제점을 해결하기 위해 나온 것이 Momentum이다. Momentum은 쉽게 말해서 가중치가 업데이트되는 방향에 가속도를 붙이는 것이다. 식을 보면 gradient는 따로 계산해두고, (Momentum Variable) x (이전 momentum) + gradient를 계산하는 것을 볼 수 있다. 그리고 이 결과물로 나온 vx를 x를 갱신할 때 곱해준다. 식은 x += lr* vx로 되어 있지만 이를 풀면 x += lr * (rho * vx) + lr * dx 가 된다. 즉 기존 SGD에서 쓰던 방식인 lr * dx에 lr * (rho * vx)가 더해져 바로 이전 갱신에서 사용된 vx가 현재 갱신에도 영향을 미치는 것이다. 이 때 rho로는 보통 0.9정도를 사용한다고 한다.
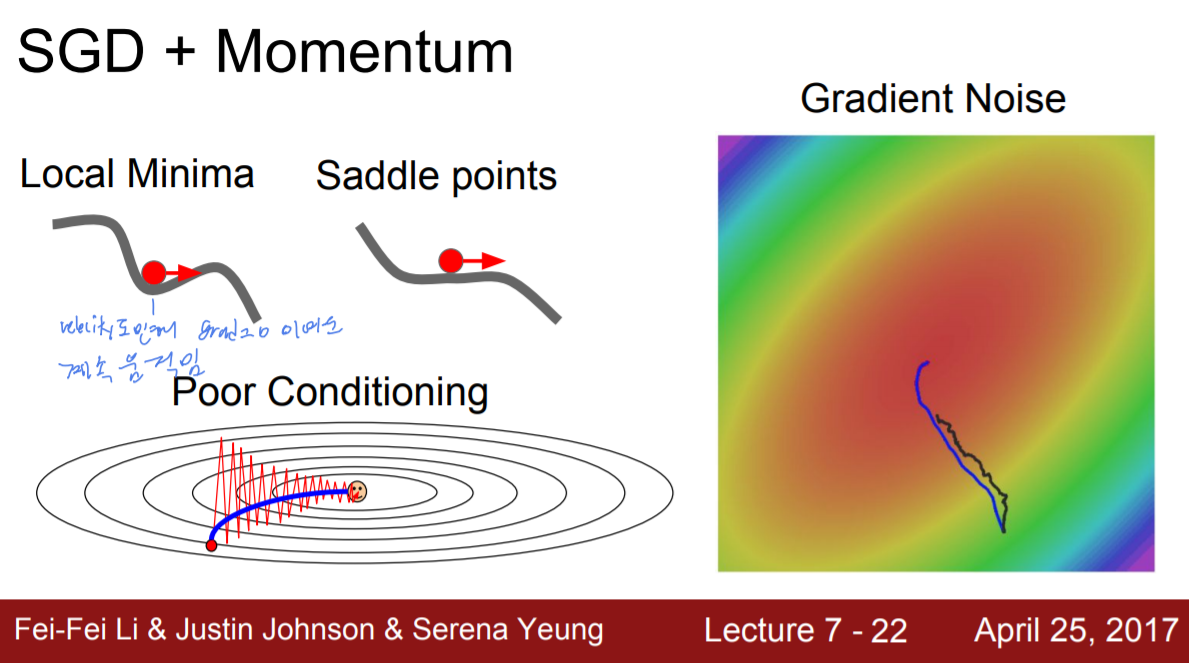
그림을 보면 Momentum을 사용함으로써 local minima와 saddle point에 빠지지 않고 지나갈 수 있음을 알 수 있다. 왜냐하면 기존 갱신이 현재 갱신에 영향을 미치기 때문이다.(관성과 비슷하다고 생각하면 될 것 같다). 또한 진동현상이 나타날 시에도 그림만큼 매끄럽지는 못하겠지만, 진동의 폭이라던가 진동 횟수 등이 현저히 감소할 것이다.
Nesterov Momentum
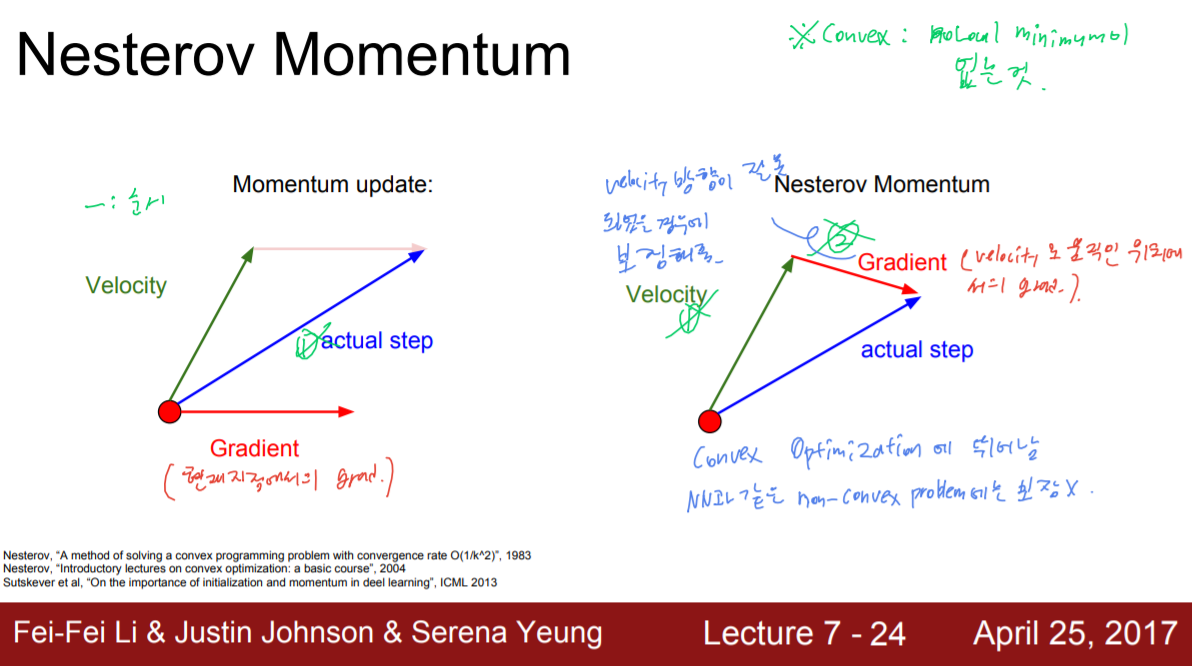
기존 Momentum같은 경우 업데이트를 할 때 velocity(vx)와 gradient(dx)가 한번에 합쳐져서 진행되었다. 그러나 만약 velocity가 안좋은 방향으로 큰 값을 가지는 경우, 이 때문에 오히려 학습이 느려질 수 있다는 문제가 있다. 이를 해결하고자 등장한 것이 Nesterov Momentum이다. Nesterov Momentum은 업데이트 시에 Velocity와 Gradient를 한 번에 계산하지 않고, 먼저 Velocity로 움직인 다음, 그 자리에서 gradient를 계산하여 gradient만큼 다시 움직이는 것이다. 이를 통해 Velocity를 보정하는 역할을 할 수 있다. 이는 보통 Convex Optimization에는 뛰어나지만 Neural Network와 같은 non-convex problem에서는 보장할 수 없다고 하는데, 이 때 Convex 는 Local minimum이 없는 것을 뜻한다.

Nesterov Momentum에 대한 자세한 식이다. 처음 봤을 때 생각보다 이해하기 어려워서 조금 난해했다. 조금씩 풀어서 보자면, 우선 현재 시점에서 구하고자 하는 것(업데이트될 결과물)은 x_t+1이며 x_t에서 x_t+1로 업데이트하기 위해 사용되는 것이 v_t+1이다. v_t+1을 계산하기 위해서 우선 x_t로 갱신될 때 사용되었던 v_t에 Momentum variable인 p를 곱한 값을 구한다. 그리고 x_t에서 이 pv_t만큼 움직인 위치를 구한 뒤, 이 위치에서의 기울기를 구한다. 이 기울기에 Learning rate인 a(알파)를 곱한 뒤 아까 구한 pv_t에서 이 값을 빼주는 것이다. 이렇게 보면 이전에 말했던 "Velocity만큼 움직인 뒤, 움직인 위치에서의 gradient만큼 움직인다"라는 것이랑 동일하다는 것을 알 수 있다.
'머신러닝&딥러닝 > cs231n' 카테고리의 다른 글
| [CS231n - Lecture 6] Training Neural Networks - Part I-2 (0) | 2021.08.02 |
|---|---|
| [CS231n - Lecture 6] Training Neural Networks - Part I (0) | 2021.07.30 |
| [CS231n - Lecture 5] Convolutional Neural Network (0) | 2021.07.28 |
| [CS231n - Lecture 4] Backpropagation and Neural Networks (0) | 2021.07.27 |
| [CS231n - Lecture 3] Loss Functions and Optimization (0) | 2021.07.14 |




