| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- dijkstra
- 클린코드
- 딥러닝
- 알렉스넷
- 1107번
- 1916
- Alexnet
- 논문
- 1261
- 백준
- 알고리즘
- 논문리뷰
- Java
- 백준 1916 자바
- 자바
- GPT
- 백준9095
- MachineLearning
- 짝지어제거하기
- NLP
- 머신러닝
- 관심사분리
- 다익스트라
- 백준 1339 자바
- 3745
- 백준 1339
- deeplearning
- 논문구현
- cs231n
- 디미터법칙
- Today
- Total
산 넘어 산 개발일지
[CS231n - Lecture 3] Loss Functions and Optimization 본문
Loss Functions
1. Multiclass SVM loss
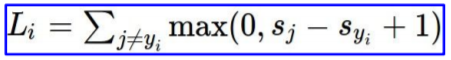
설명
Multiclass SVM loss는 정답 score와 비정답 score 간의 차이로 손실함수를 계산하는 방식이다. 이 때 중요한 점은 score의 정확한 값보다는 정답 scroe와 비정답 score간의 상대적인 차이에 집중한다는 점이다.
시그마에서 j = yi를 빼는 이유는 Loss의 이론적 최소 값을 0으로 맞추기 위함이다. 만약 j = yi가 식에 포함된다면, Sj - Syi + 1 = 1이 되므로 Loss의 최소 값이 0이 될 수 없다.
디버깅
초기 W의 설정은 주로 0과 비슷한 작은 값으로 설정한다. 즉 Sj 와 Syi가 매우 흡사해지므로, 초기 W가 잘 설정되어 있다면 Total loss = (Class 개수) - 1 이라는 것을 알 수 있다. 모델 훈련 시, 이를 통해 초반에 디버깅을 진행할 수 있다.
2. Regularization

Regularization(정규화)는 모델의 Overfit을 방지하기 위해 사용한다. 즉 너무 복잡한 그래프가 되어 Training data에만 적합한 모델이 되는 것을 방지하는 것이다. Training Data에 지나치게 fit할 경우, 적절한 패널티를 주어 "이 Value라고 예측하고 싶으면 이정도의 패널티를 감수해라!" 라고 말하는 것이다. 이를 통해 그래프가 조금 더 매끄럽게(혹은 단순하게) 되어 overfit을 예방할 수 있다.
주로 사용되는 Regularization들은 다음과 같다.
- L2 Regularization
- L1 Regularization
- Elastic net (L1 + L2)
- Dropout
- Batch Normalization
3. Softmax Classifier(Multinomial Logistic Regression)

설명
Softmax는 각 score를 계산한 뒤, 이를 지수에 활용함으로써 양수로 만든다. 이후 이 값들을 활용하여 확률분포의 형식으로 표현하는 것이다. 여기서 구한 확률분포는 -log를 취함으로써 Loss로 사용할 수 있는데, 이 Loss 식은 확률분포가 [1, 0, 0, ..]이 되도록 유도한다. 또한 Log를 사용하는 이유는 Log를 최대화하는것이 그냥 확률값을 최대화하는 것보다 쉽기 때문이다.
Multiclass SVM Loss와의 가장 큰 차이점은 SVM Loss에서는 정답 score와 비정답 score의 차이에 집중한 반면, Softmax에서는 score 자체에 집중한다는 점이다. 왜냐하면 이 score 값 하나하나가 결국 확률분포를 이루고, 이 확률분포가 Loss에 사용되기 때문이다.
디버깅
초기 W 설정 시에 모든 W가 0과 가깝다. 그렇기에 모든 S들도 0과 비슷하므로, 초기 Loss는 -log(1/C) = log(C)와 비슷해야 한다. (C : Class 개수) 이를 활용하여 처음 W설정이 잘 되었는지, 버그가 있지는 않은지를 디버깅할 수 있다.
Optimization
1. Gradient(기울기)
손실함수 Loss의 각 지점에서, 각 순간의 기울기를 사용하여 손실함수가 적어지는 부분으로 이동할 수 있다. 이 때, 이를 하나하나 이동해보며 선택하기보다는, 하나의 식을 세우고 이를 미분하여 이동하는 것이 효율적이다.

2. Stochastic Gradient Descent (SGD)
기울기를 사용하여 제일 낮은 손실을 찾아가는 것은 좋다. 그러나 만약 데이터의 개수 N이 너무 크다면 어떨까? 미분을 사용하여 한 걸음 나아가기 위해서 이 모든 N을 돌아봐야 하기 때문에 상당히 비효율적이다. 그래서 등장한게 SGD이다. SGD에서는 minibatch라는 것을 만들어, 기존의 N개의 데이터에서 몇 개의 샘플만 가져온다. 그 후, 이 샘플들만을 사용하여 미분을 계산하고 한 걸음 나아가는 것이다. 물론 모든 데이터를 보지 않는다는 점에서 항상 올바른 방향으로 나아간다는 보장은 없지만, 훨씬 빠르기 때문에 여러 번 반복하면 결국 minibatch를 사용하지 않았을 때와 비슷하게 수렴한다.
출처 : https://www.youtube.com/c/stanfordengineering/featured
Stanford University School of Engineering
The Stanford School of Engineering has been at the forefront of innovation for nearly a century, creating pivotal technologies that have transformed the worlds of information technology, communications, medicine, energy, business and beyond. The faculty, s
www.youtube.com
'머신러닝&딥러닝 > cs231n' 카테고리의 다른 글
| [CS231n - Lecture 7] Training Neural Networks - Part II (0) | 2021.08.11 |
|---|---|
| [CS231n - Lecture 6] Training Neural Networks - Part I-2 (0) | 2021.08.02 |
| [CS231n - Lecture 6] Training Neural Networks - Part I (0) | 2021.07.30 |
| [CS231n - Lecture 5] Convolutional Neural Network (0) | 2021.07.28 |
| [CS231n - Lecture 4] Backpropagation and Neural Networks (0) | 2021.07.27 |




