| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- GPT
- 백준
- 클린코드
- 백준 1339 자바
- Java
- 알고리즘
- 자바
- 1916
- Alexnet
- 알렉스넷
- 1261
- MachineLearning
- 짝지어제거하기
- 3745
- 다익스트라
- 딥러닝
- 1107번
- 관심사분리
- 논문구현
- 백준 1339
- 머신러닝
- 백준9095
- 논문리뷰
- dijkstra
- 논문
- NLP
- 백준 1916 자바
- cs231n
- deeplearning
- 디미터법칙
- Today
- Total
산 넘어 산 개발일지
[CS231n - Lecture 6] Training Neural Networks - Part I 본문
[CS231n - Lecture 6] Training Neural Networks - Part I
Mountain96 2021. 7. 30. 16:01Activation Functions

Activation function은 한 뉴런(혹은 레이어)에서 값을 출력할 때 사용되는 함수이다. 즉 가장 최종적인 연산이라고 생각하면 된다. 이 Activation function에도 여러 종류가 있다. 가장 최초로 나온 것은 Sigmoid이며, 이에 대한 보완책으로 여러 함수들이 개발되었다. 이 함수들에 대해서 각각 어떤 문제점을 보완했는지, 단점은 무엇이 남아있는지를 공부하고자 한다.
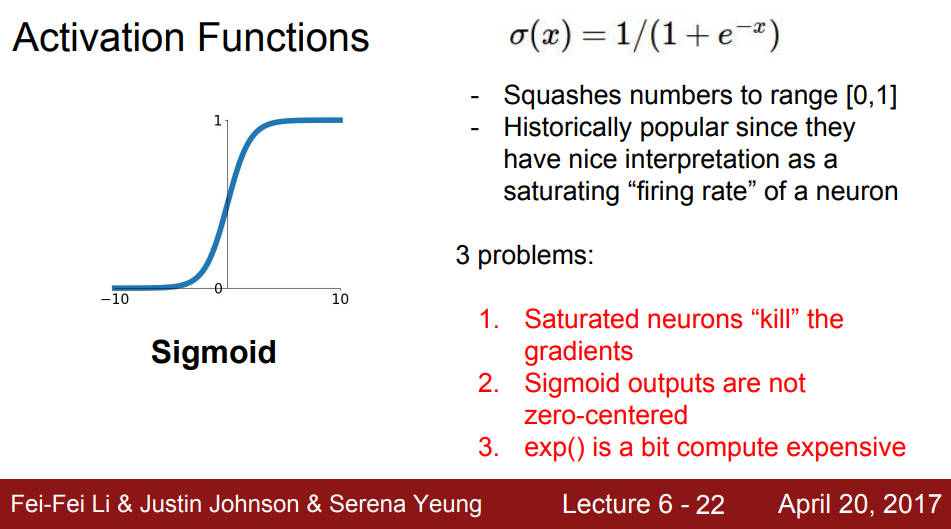
Sigmoid 함수는 일정한 범위 내에서(약 [-4, 4])는 선형적인 모습을 보이지만, 이를 벗어나면 비선형적인 모습을 보인다. 이는 뉴런의 "firing rate"를 적절히 해석했다는 점에서 장점이 있지만, 3가지 단점이 있다.
첫 번째는 saturate 되는 부분, 즉 뉴런의 값이 극단적으로 높거나 낮아지는 부분들이 기울기가 0에 수렴한다는 점이다. 기울기가 0이면 무엇이 안좋을까? 예를 들어 뉴런의 출력값이 0이였다고 해보자. 이 경우 네트워크에 문제는 없다. 그러나 출력값이 -10이거나 10일 경우, 역전파 시 이 부분의 기울기, 즉 0을 사용해서 역전파를 진행하게 된다. 역전파에 0이 곱해지는 경우 뉴런의 값도 비정상적으로 작아지고, Vanishing Gradient문제가 발생하게 된다.
두 번째는 출력값들이 zero-centered하지 않다는 점이다. zero-centered란 함수로 나올 수 있는 출력결과의 중간이 0으로 맟추어져 양수를 출력할 수도 있고 음수를 출력할 수도 있는 상태를 의미한다. Sigmoid의 상태에선 출력결과가 0이상이 나올 수밖에 없다. 이것이 왜 문제가 될까?

이 또한 역전파 부분에서 문제가 생긴다. 뉴런에 대한 input이 모두 양수인 경우를 생각해보자. 한 뉴런을 기준으로 볼 때. 위에서 내려온 미분값은 양수 혹은 음수를 가질 것이다. 그리고 우리의 식은 f=Wx + b이므로 W를 업데이트하기 위해서 W에 대한 미분을 진행하면 f'=x 가 된다. 이는 W에 대한 local gradient이므로, W에 대한 결과값의 미분을 알기 위해서는 local gradient(f'=x)와 위에서 내려온 미분값(양수 혹은 음수)을 곱해야 한다. 그러나 x가 양수이므로, 이 미분값의 부호는 위에서 내려온 미분값의 부호와 같아지게 된다. 결국 모든 전체 W의 원소들은 같은 부호를 가질 것이다. 즉 W는 항상 같은 방향으로만 업데이트가 될 수밖에 없다. 위 슬라이드의 우측 그래프를 보면, 파란색 최종점에 도달하기 위해 빨간색 path가 삽질하는 모습을 볼 수 있다. 이는 W가 모두 음수일 때 [아래 + 좌측]으로, 모두 양수일때 [위 + 우측]으로 이동하는 모습이다. 따라서, 목적지에 도달하기까지 최적화된 길로 이동하지 못하고, 삽질을 하면서 이동해야 하기 때문에 비효율적으로 가중치가 업데이트되는 것이다.
세 번째는 sigmoid 식에 쓰이는 exp()가 비싼 연산이라는 점이다.
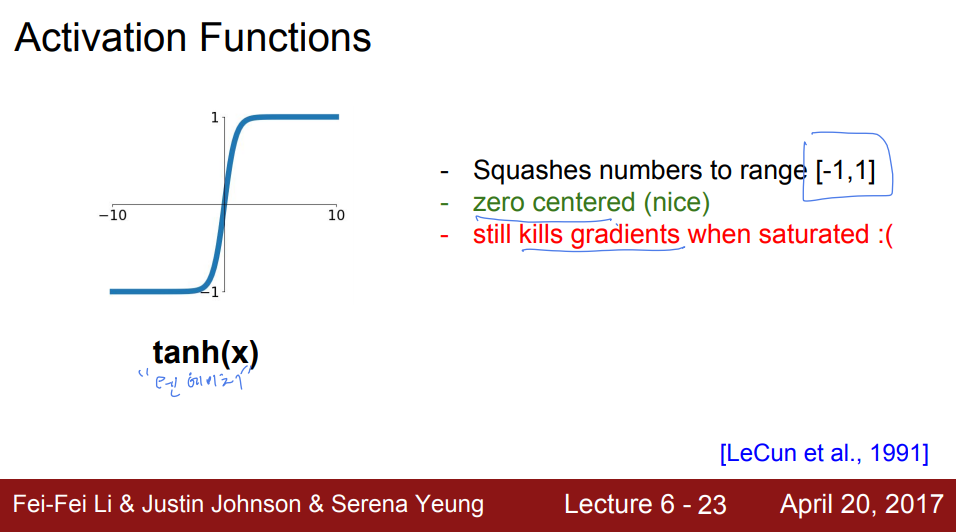
다음으로 볼 함수는 tanh 함수이다. tanh는 기존 sigmoid가 zero-centered하지 못하다는 단점을 보완한 함수이다. 그러나 여전히 Saturate되는 부분에서 gradient가 0이 되어 Vanishing Gradient문제를 해결하지 못하였다.
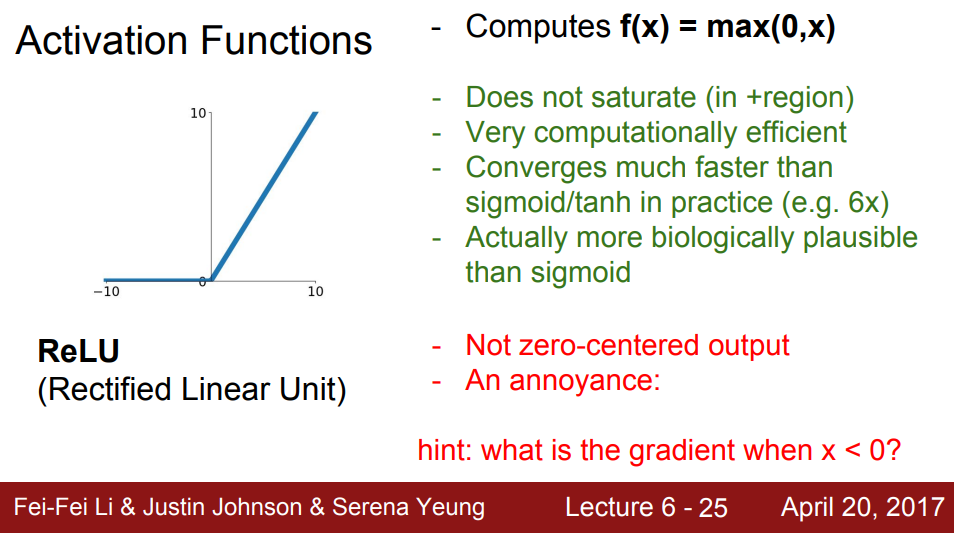
ReLU는 아마 현재 가장 많이 쓰이는 함수일 것이다. 이는 다음과 같은 다양한 장점이 있다.
- 양수 부분에서 Saturate하지 않는다. (Vanishing Gradient 일부 방지)
- 계산비용이 적다 (exp()를 사용하지 않고, 식이 간단하므로)
- sigmoid, tanh보다 훨씬 빨리 수렴한다.
- 생물학적 원리와 어느정도 상응한다.
그러나 zero-centered문제를 해결하지는 못했고, 여전히 음수 부분에서는 Saturate하다는 단점이 존재한다. 또한 Dead ReLU라는 단점도 존재한다.
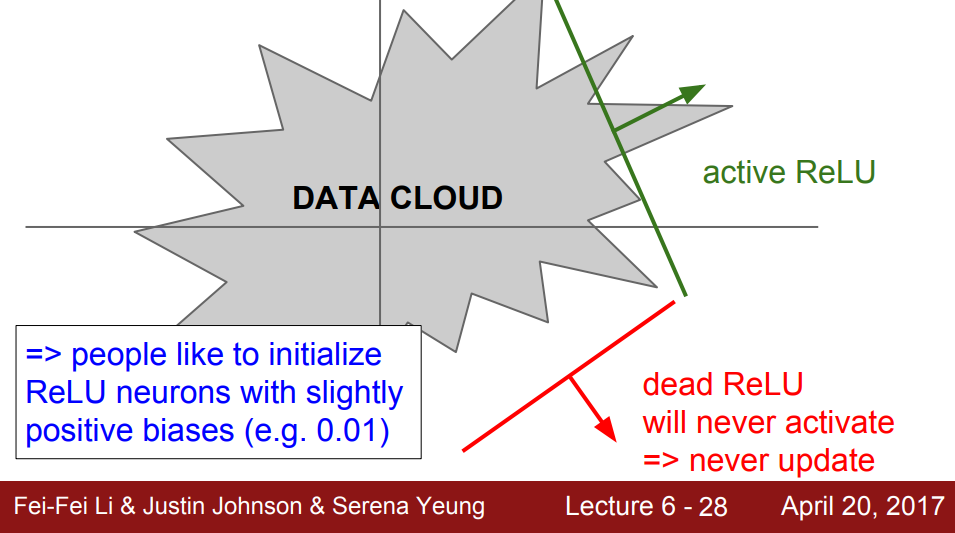
Dead Relu는 ReLU가 Data Cloud로부터 지나치게 멀어져 있을 때 발생하는 현상이다. 이 경우, 뉴런이 활성화되지 않아서 전혀 업데이트가 되지 않는 문제가 발생한다. 이같은 일이 발생하는 이유로는 2가지 정도가 있다.
1. 초기화를 잘못한 경우
즉 초기 가중치가 Data Cloud로부터 너무 멀어져 있으면, 활성화가 되지 않아 업데이트되지 않는다.
2. Learing rate가 너무 높은 경우
learning rate가 너무 높을 경우, 학습 도중 갑자기 튀어서 Data Cloud과 너무 멀어지는 현상이 발생할 수 있다. 이같은 현상은 생각보다 자주 발생한다고 한다.
이를 해결하기 위해 사람들은 초기화 시 약간의 positive bias를 준다고 한다. 예를 들어 0.01정도를 주어서 초기화로 인한 Dead ReLU 현상을 막아보려는 것이다. 그러나 이것이 도움이 되는지 안되는지에 대해서는 아직 논의중이다.
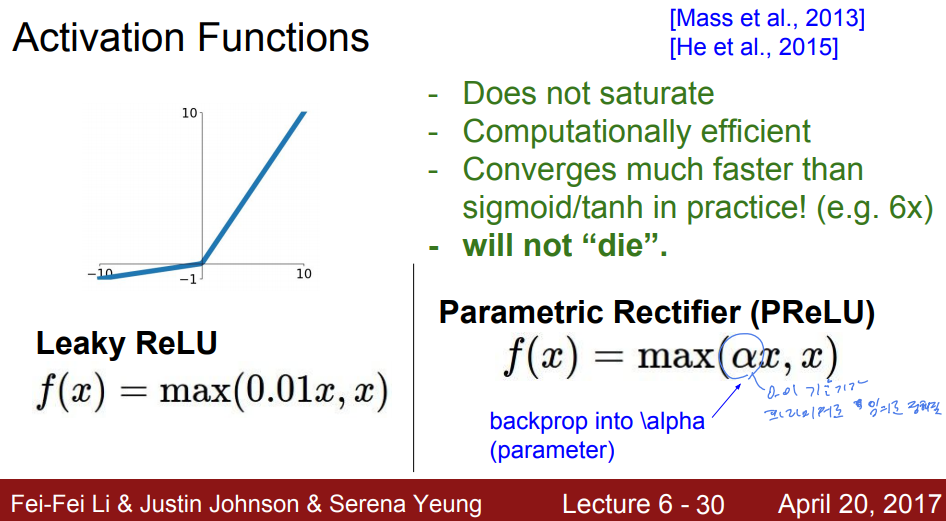
다음은 Leaky ReLU이다. 이름에서 알 수 있듯이 ReLU에 약간의 변형을 가한 것이다. ReLU에서 음수 영역의 Saturate현상을 보완했다. 특히, 뉴런이 죽지(Die) 않는다는 것이 가장 큰 장점일 것이다. 식에서 쓰이는 기울기인 α는 하이퍼파라미터로 임의로 정해줄 수 있다.
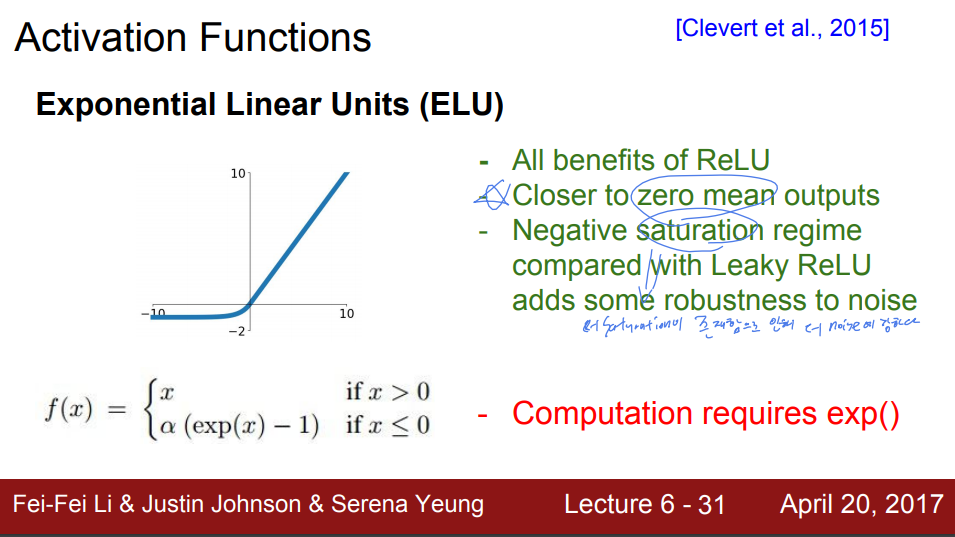
다음은 ELU이다.(Lu 패밀리..) ReLU의 모든 장점들을 가지고 있고, 출력값이 zero-mean에 가깝다는 장점이 있다. 또한, Leaky ReLU와 비교했을 때, 음의 영역에서 Satuartion이 다시 발생하는데, 오히려 이 Saturation이 존재함으로 인해서 noise에 더 강하다고 한다. 그러나 exp()를 식에서 사용하기 때문에 계산비용이 크다는 단점이 있다.
Data Preprocessing
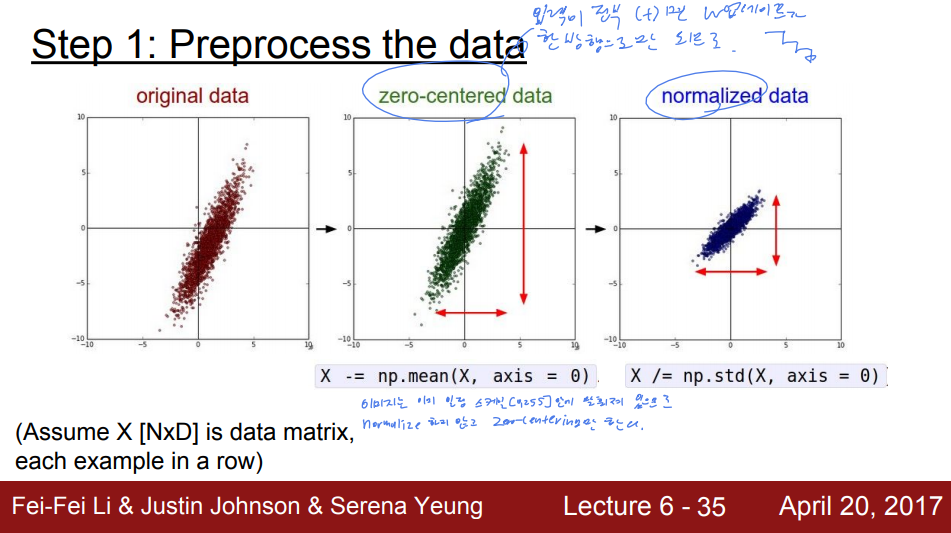
Zero-Center
입력이 전부 (+) 일 경우 Sigmoid에서의 두 번째 단점처럼 학습이 최적의 경로로 진행되지 않는다.
Normalization
값의 범위를 0~1사이로 맞춰준다
그러나 이미지의 경우 이미 [0, 255] scale로 맞춰져 있으므로 굳이 진행할 필요는 없다.
정규화? 표준화?
딥러닝을 공부하다보면 정규화, 표준화와 같은 용어들이 쓰이는데, 정확히 어떤 개념이고 어떻게 구분되는지 항상 헷갈린다. 이번 기회에 한번 정리해보고자 한다.
Normalization
값의 범위를 [0, 1]사이로 맞추는 것
효과
- Scale이 너무 큰 feature의 영향이 커지는 것 방지
- Local Minimum에 빠질 확률 감소(+ 학습 속도 향상)
식 : (X - X_min) / (X_max - X_min)
Standardization
평균이 0, 분산(혹은 표준편차)이 1이 되도록 하는 것
효과
- Scale이 너무 큰 feature의 영향이 커지는 것 방지
- Local Minimum에 빠질 확률 감소(+ 학습 속도 향상)
특이하게, Standardization은 (정규분포 - > 표준정규분포)의 변환으로도 해석될 수 있다.
- [-1, 1]에 68%의 데이터가, [-2, 2]에 95ㅆ의 데이터가, [-3, 3]에 99%의 데이터가 있다.
- [-3, 3]의 범위를 벗어나느 것은 이상치(outlier)일 확률이 높다.
식 : (X - 평균) / 표준편차
Regularization
Weight(가중치)에 제약을 가하는 방법
효과
- Overfit 방지
예시 : L1, L2, ...
출처 : https://www.youtube.com/c/stanfordengineering/featured
Stanford University School of Engineering
The Stanford School of Engineering has been at the forefront of innovation for nearly a century, creating pivotal technologies that have transformed the worlds of information technology, communications, medicine, energy, business and beyond. The faculty, s
www.youtube.com
'머신러닝&딥러닝 > cs231n' 카테고리의 다른 글
| [CS231n - Lecture 7] Training Neural Networks - Part II (0) | 2021.08.11 |
|---|---|
| [CS231n - Lecture 6] Training Neural Networks - Part I-2 (0) | 2021.08.02 |
| [CS231n - Lecture 5] Convolutional Neural Network (0) | 2021.07.28 |
| [CS231n - Lecture 4] Backpropagation and Neural Networks (0) | 2021.07.27 |
| [CS231n - Lecture 3] Loss Functions and Optimization (0) | 2021.07.14 |




