| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 클린코드
- 1261
- GPT
- 알고리즘
- 1107번
- Java
- 백준9095
- deeplearning
- 백준 1339 자바
- 디미터법칙
- 자바
- 논문
- Alexnet
- 백준 1339
- 알렉스넷
- NLP
- 백준 1916 자바
- 짝지어제거하기
- 논문구현
- 딥러닝
- 3745
- dijkstra
- 논문리뷰
- 관심사분리
- 머신러닝
- 백준
- 다익스트라
- cs231n
- 1916
- MachineLearning
- Today
- Total
산 넘어 산 개발일지
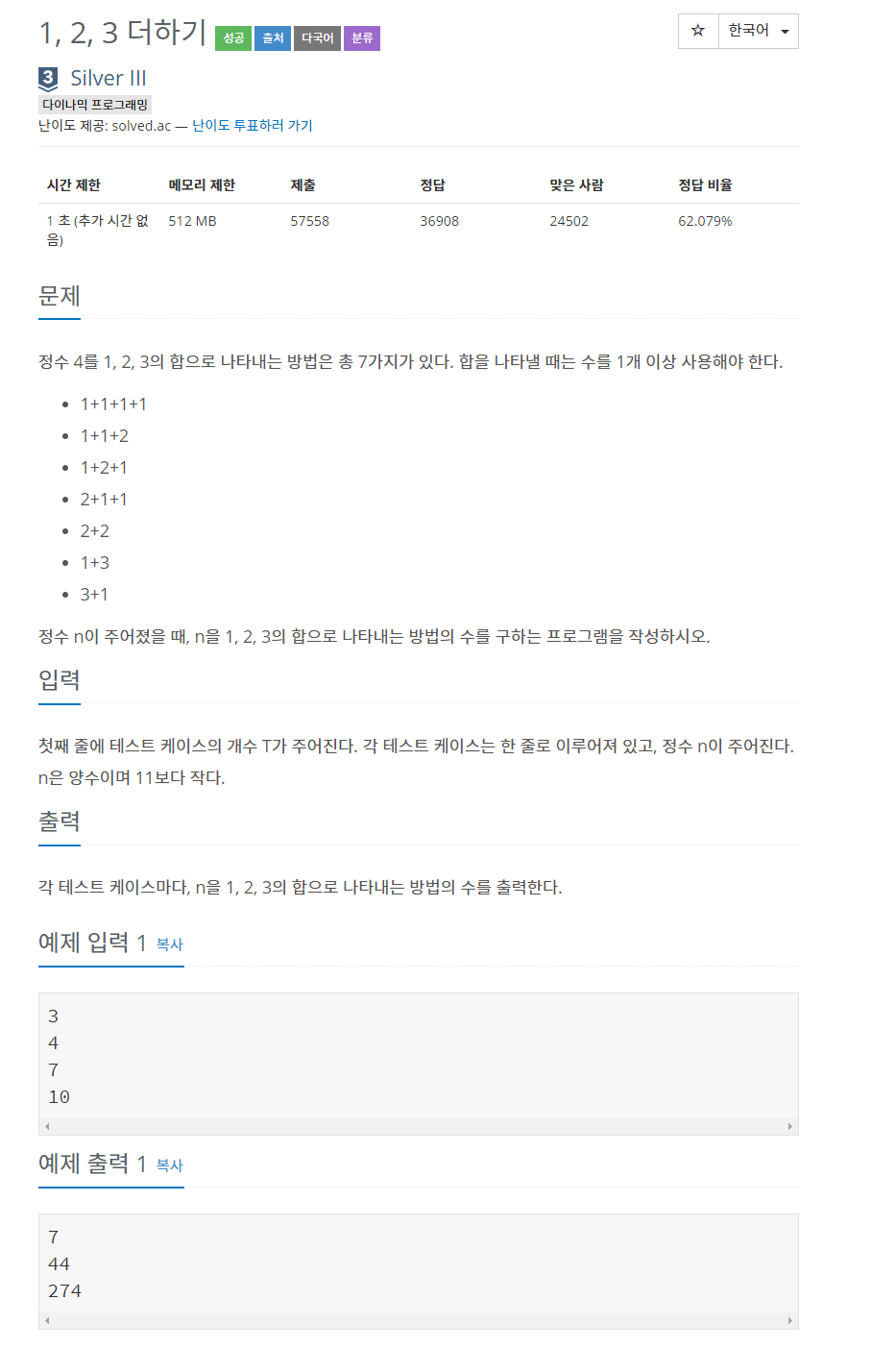
[백준] 9095번 - 1, 2, 3 더하기 (Java) 본문
풀이
키워드
- DP
숫자들을 사용해 나가는 DP 문제는 대부분 이전 숫자들을 이용하는 것이 많다. 즉 dp[i]를 구하기 위해서는 dp[i-1] 이나 dp[i-2] 등을 이용하는 것이다. 이번 문제도 크게 다르지 않았다.
먼저, 이번 문제의 특별한 숫자들로는 1, 2, 3이 있다. 이 숫자들을 사용해 앞으로의 숫자들에 대한 덧셈 식을 구현하는 것이다. 따라서, 먼저 이 숫자들이 몇 개의 덧셈식을 가지고 있는지를 계산해놓자.
- dp[1] = 1 (1)
- dp[2] = 2 (1+1, 2)
- dp[3] = 4 (1+1+1, 1+2, 2+1, 3)
이제 4를 보자. 4는 문제에 나와있듯이 7개의 덧셈식이 존재한다.
- 1+1+1+1
- 1+1+2
- 1+2+1
- 2+1+1
- 2+2
- 1+3
- 3+1
이를 맨 뒤 숫자만 제외하고, 될 수 있는 대로 1, 2, 3으로 묶어보자.
- 3+1
- 2+2
- 3+1
- 3+1
- 2+2
- 1+3
- 3+1
(3+1)이 4개, (2+2)가 2개, (1+3)이 1개가 나온다. 즉 숫자 4가 되는 덧셈식들은 사실 "(3이 될 수 있는 덧셈식) + 1", "(2가 될 수 있는 덧셈식) + 2", "(1이 될 수 있는 덧셈식) + 3" 인 것이다. 따라서 dp[4] = 4+2+1 이 성립한다.
이는 5, 6, 7, ...에도 동일하게 적용된다. 5를 예로 들어보자
5의 경우 (4+1), (3+2), (2+3)이 나온다.
((1+4)는 제외한다. 왜냐하면 덧셈식을 구성하는 숫자는 1, 2, 3뿐이므로, "(1이 될 수 있는 덧셈식) + 4"는 존재할 수 없기 때문이다.)
따라서, 숫자 5가 되는 덧셈식은 "(4가 될 수 있는 덧셈식) + 1", "(3이 될 수 있는 덧셈식) + 2", "(2가 될 수 있는 덧셈식) + 3" 이므로 dp[5] = dp[4] + dp[3] + dp[2] = 7+4+2=13이 성립한다.
이를 통해 우리가 알 수 있는 점화식은
dp[i] = dp[i-1] + dp[i-2] + dp[i-3] (단, i > 3)
이다.
코드
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
public class Main {
static int [] dp = new int[11];
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
int T = Integer.parseInt(br.readLine());
dp[1] = 1;
dp[2] = 2;
dp[3] = 4;
for(int i = 4; i < 11; i++) {
dp[i] = dp[i-1] + dp[i-2] + dp[i-3];
}
while(T-- > 0) {
int n = Integer.parseInt(br.readLine());
sb.append(dp[n]).append("\n");
}
System.out.print(sb);
}
}
출처 : www.acmicpc.net/problem/9095
9095번: 1, 2, 3 더하기
각 테스트 케이스마다, n을 1, 2, 3의 합으로 나타내는 방법의 수를 출력한다.
www.acmicpc.net
'알고리즘 > 백준' 카테고리의 다른 글
| [백준] 1644번 - 소수의 연속합(Java) (0) | 2021.05.14 |
|---|---|
| [백준] 1107번 - 리모컨(Java) (0) | 2021.04.14 |
| [백준] 1916번 - 최소비용 구하기 (Java) (0) | 2021.04.07 |
| [백준] 1339번 - 단어 수학 (Java) (0) | 2021.04.06 |
| [백준] 14500번 - 테트로미노 (Java) (0) | 2021.04.05 |




